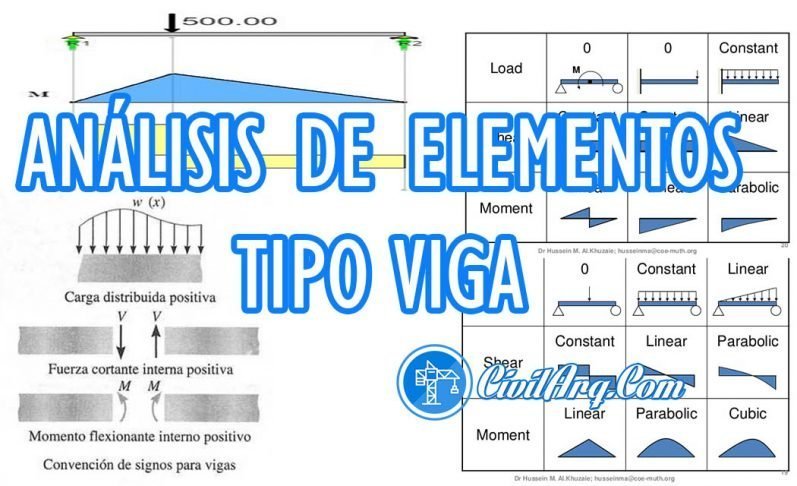
Objetivo: Determinar la respuesta (fuerzas internas y deformaciones) en elementos tipo viga.
Los modelos estudiados hasta ahora involucraban la estabilidad y equilibrio externo de la estructura. Para completar el análisis se hace necesario el conocimiento de las fuerzas internas en cada uno de los elementos que componen el sistema estructural. En este caso nos referiremos a los elementos tipo viga.
Sabemos que en los elementos tipo viga las fuerzas internas involucran tres incógnitas: una fuerza axial, una fuerza cortante y un momento, por lo tanto conociendo las fuerzas de extremo y aplicando el método de las secciones en cualquier punto de la viga nos daría como resultado un tramo de viga estáticamente determinado con tres ecuaciones estáticas disponibles y tres incógnitas por determinar. Observemos que la clave es conocer las fuerzas de extremo de elemento, es decir, aquellas que se ejercen en las uniones con otros elementos pertenecientes al sistema estructural y de ahí proceder a determinar las fuerzas internas por la estática. Podemos concluir que el elemento a analizar es estáticamente determinado así pertenezca a un sistema indeterminado.
Esto explica porque la metodología y el objetivo de los métodos de análisis es determinar las fuerzas de unión y de ahí seguir con el análisis independiente de cada elemento.
Teniendo en cuenta estas consideraciones podemos aislar un elemento tipo viga, considerarlo con sus fuerzas extremas como fuerzas de reacción y analizarlo hasta encontrar las fuerzas internas:
Notemos que al partir el elemento una sección ejerce sobre la otra fuerzas equivalentes a un apoyo de empotramiento, podemos decir, que las conexiones que se generan a lo largo del elemento son uniones rígidas y las fuerzas en cada sección son iguales y de sentido contrario.
Para el estudio de los elementos tipo viga se utilizará la siguiente convención:
Cortante: Las fuerzas cortantes positivas son aquellas que producen una rotación horaria del elemento
Momento: Los momentos positivos son aquellos que producen concavidad hacía arriba en el elemento horizontal o tracciones en la fibra inferior. Para elementos verticales esta convención se puede complicar un poco por lo tanto regirá el criterio de dibujar el diagrama de momentos para la cara traccionada.
Fuerza axial: Se considera una fuerza axial positiva cuando ella implica tracción en el elemento.
Las acciones de las fuerzas internas en vigas se ilustran mejor por medio de diagramas de fuerza axial (P), diagramas de fuerza cortante (V) y diagramas de momento flector (M). Los diagramas representan la variación de estas fuerzas a lo largo del elemento, dibujando en las abcisas la longitud del elemento y en las ordenadas el valor de la fuerza interna. Para axial y cortante los valores positivos se dibujan por encima del elemento pero para los momentos se dibujará el diagrama para el lado traccionado del elemento, así, si el elemento es horizontal el lado positivo del diagrama estará para abajo. La convención para momentos rige para cualquier ubicación de este en el espacio y es independiente del origen escogido, ya sea este en el extremo derecho o izquierdo del elemento.
Relación entre momento cortante y carga
En el caso de cargas distribuidas actuando perpendicular al elemento se puede encontrar una relación con las fuerzas internas de cortante y momento por medio del siguiente análisis de una sección infinitesimal del elemento.
Aplicando equilibrio a la sección de viga indicada tenemos:
integrando a ambos lados, tenemos:
la variación del cortante en un tramo de viga dado es igual al área bajo la curva de carga. (note que el equilibrio se hizo con la carga negativa, por lo tanto no se debe involucrar otra vez su signo en la ecuación).
dividiendo por dL a ambos lados tenemos:
, donde podemos decir que la pendiente a la curva del diagrama de cortante es igual al negativo de la carga distribuida.
Ahora con la ecuación de momentos tenemos:
considerando una longitud muy pequeña del trozo de viga analizado, el término con dL2 se aproxima a cero, y la ecuación nos queda
integrando:
de donde la segunda integral representa el área bajo la curva del diagrama de cortantes en un tramo de viga dado y podemos concluir que la variación del diagrama de momentos en un tramo de vigas es igual al área bajo la curva del diagrama de cortante.
Dividiendo a ambos lados por dL, tenemos:
donde la pendiente del diagrama de momentos en cualquier punto es igual al valor del cortante en ese punto.
Ejercicios
Dibujar los diagramas de cortante, momento y curva elástica tentativa:
Para los diagramas de momento se verificará la convención haciendo el ejercicio ubicando el origen en ambos extremos del elemento. Determinar en cada caso el eje coordenado de las ordenadas de la gráfica de momentos.
De que depende la orientación del eje de momentos?. Es esta única para un elemento dado?.
Podría determinar una manera fácil de orientar los ejes en elementos verticales y horizontales de acuerdo con la convención fijada. Cómo sería esa orientación en un marco?.
En las estructuras tipo marco se sugiere trabajar encontrando primero las fuerzas de extremo de los elementos y después aplicar equilibrio a cada uno. Con estos ejercicios se pretende que el estudiante tomo conciencia de los momentos de continuidad en los nudos.
Viga simplemente apoyada:
Tomaremos el ejemplo de un elemento simple, con fuerzas de extremo equivalentes a uniones de articulación.
Se pide encontrar los diagramas de momento y corte.
Se debe partir por encontrar las fuerzas de extremo del elemento y se recalca que el elemento, así pertenezca a un sistema estructural compuesto, debe estar en equilibrio estático, cumplir con las ecuaciones de equilibrio, considerando tanto las fuerzas de extremo o unión al sistema como las fuerzas externas actuando sobre él.
Ø Fuerzas de reacción:
Ø Fuerzas internas: Aplicación del método de las secciones.
Note que el término es la sección en el extremo izquierdo del elemento, por lo tanto este se puede expresar como
Construcción del diagrama de corte:
- Sabemos que el elemento está en equilibrio por lo tanto el diagrama empieza en cero y termina en cero.
- Cuando hay fuerzas puntuales estas implican un brinco igual a su valor en el diagrama de corte (variación brusca de este), el brinco se da en la misma dirección de la carga puntual aplicada.
- Recordemos que el valor –w es la pendiente del diagrama de cortante.
Empezando por el lado izquierdo tenemos:
Notemos que la sección del extremo se convierte en el cortante, así podríamos decir que Va = Ay y Vb = By.
Punto donde el corte es cero:
Si entonces igualando V = 0 y despejando x, tenemos:
el punto de cortante cero se encuentra dividiendo el cortante de extremo por la carga w.
Otra relación interesante es que nosotros podemos obtener el cortante en cualquier punto restando al cortante de extremo lo que llevamos de carga encima del tramo estudiado (w.x).
Construcción del diagrama de momentos:
Ø El diagrama empieza en cero y termina en cero.
Ø Cuando hay momentos de extremo o puntuales se interrumpe la continuidad del diagrama presentándose un brinco en éste. Si el momento puntual es positivo, el brinco será negativo y viceversa.
Ø Recordemos que el valor del cortante es igual a la pendiente del diagrama de momentos.
Retomando el ejemplo inicial y empezando por el lado izquierdo de la viga tenemos:
Según la convención fijada los momentos positivos producen tracciones en la parte inferior, por eso se coloca el eje positivo para abajo.
Notemos que con las pendientes se puede trazar fácilmente el diagrama de momentos, inclusive nos muestra la curvatura.
Sabemos que un momento positivo produce concavidad hacia arriba, por lo tanto la curvatura será hacia arriba.
Determinemos el valor del momento máximo considerando que este se presenta cuando el cortante es cero (siempre una pendiente igual a cero muestra los puntos máximos y mínimos de una curva).
* cuando
, reemplazando en la ecuación de momentos tenemos:
para
Otros tipos de vigas:
CORTE MOMENTO
PUNTOS CRÍTICOS EN UN DIAGRAMA DE MOMENTOS:
Asumiendo que los elementos estudiados pertenecen a un sistema estructural complejo, analizaremos una viga con momentos en ambos extremos que representan la unión con otros elementos o su continuidad después de un apoyo.
MARCOS CONFORMADOS CON ELEMENTOS TIPO VIGA
En cada uno de los siguientes marcos determine reacciones externas, fuerzas de extremo de elementos y diagramas de momento, cortante y axial.
Analice en cada uno de los elementos si es posible encontrar elementos donde exista M y no exista V. Es posible que un elemento tenga momentos si está sometido a carga axial solamente. Concluya.
EJES LOCALES:
Después de trazar los diagramas de fuerzas internas de varias estructuras con elementos orientados de diferentes maneras podemos concluir que el trabajo se hace mas fácil si trazamos unos ejes coordenados para cada elemento.
Si los elementos a analizar no coinciden con los ejes de coordenadas de todo el sistema, el encontrar sus fuerzas internas se puede complicar, por lo tanto se propone que cada elemento trabaje con unos ejes coordenados propios, donde el eje 1 coincide con el eje axial del elemento, el eje 2 es perpendicular al elemento y el eje 3 se fija por la regla de la mano derecha como el resultado del producto cruz (1 X 2). Estos ejes se denominan ejes locales. Notemos que los ejes locales coinciden con las fuerzas internas de axial, corte y momento respectivamente.
Cuando se analiza todo un sistema estructural nos encontramos con unos ejes coordenados generales que rigen todo el sistema de cargas y reacciones, a este sistema de ejes se le conoce como ejes globales de toda la estructura. Como resultado de un análisis general encontraremos las fuerzas en los nudos, que constituyen las fuerzas de extremo de cada elemento. Para encontrar los diagramas de fuerzas internas en cada elemento debemos transformar las fuerzas de extremo en coordenadas globales a fuerzas de extremo en coordenadas locales.
TRANSFORMACIÓN DE COORDENADAS:
Para pasar cualquier sistema de fuerzas de ejes globales a locales tenemos:
Estas ecuaciones cumplen para todos los casos siempre y cuando θ se mida desde el eje positivo de las X y en sentido antihorario.
Transformación de coordenadas para carga distribuida:
Cuando se trabaja con elementos inclinados se debe tener cuidado con el tipo de carga distribuida, ya sea esta dada en la proyección horizontal del elemento o en toda la longitud de este. Notemos que las resultantes de ambas son diferentes.
En ambas condiciones, para encontrar fuerzas internas, se debe transformar la carga a ejes locales del elemento por medio de una descomposición simple de cargas.